Math is overrated
Our mental model of value needs new priors.
It's a tough article to defend, but here goes nothing.
A few years ago, the Harvard Business Review put out a bizarre stub of research that collapsed in on itself as soon as it even began. The piece, its opening summary told us, would identify the skills we need to stay relevant in an economy that’s increasingly dominated by "mathematically-focused jobs." The answer, revealed in every MBA student’s favorite blunt analytical instrument—a series of points arbitrarily scattered across a two-by-two matrix—was not mathematics. Buzzy skills like data visualization, business intelligence, data science, and AI were on the frontiers of value and efficiency, but math—that juvenile banality, that undisruptive dullard, that legacy technology—was unceremoniously dumped in the quadrant labeled “Ignore.”
The internet, always looking for an easy mark1 to put on a poster, bulleted in for the dunk. The piece was destroyed, demolished, obliterated, eviscerated. We now trot it out on its birthday, to humiliate it for some more clicks, over and over and over again.
But what if, amid our gleeful ridicule, the post accidentally stumbled into an unexpected truth? What if math is overrated—and it’s exactly our infatuation with it that, ironically, motivated the creation of the diagram in the first place and blinds us to its inadvertent wisdom? What if our thundering dunk is actually a charge?
A homely mind
At some point when I was a teenager, I became a “math person.” I wasn’t any kind of savant—I took the same middle school math classes as everyone else; I was never a mathlete—but I had a graphing calculator and liked looking at the statistics on the backs of baseball cards, so the branding stuck. In college, because of my fear of writing and my fear of breaking character, I kept going, and majored in math.
To most of my friends and family, it made sense that I eventually found my way into a career in data. Math and data are often seen as siblings, if not outright twins. One is just the practical application of the other. Math is what you study if you want to be a data scientist; data science is what mathematicians do to make money.
But once you do the job for a while, it’s hard not to see that union as overstated, or at least outdated. Though some data roles—those that build predictive models and analyze complex multivariate tests, for example—are often neck deep in graduate-level stats, this isn’t the norm. Instead, the 99 percent of analytical jobs deal in much simpler mathematical affairs.2 Yes, we have to be numerically fluent and quantitatively comfortable, but most of the math we do is calculating sums, computing ratios, and checking if averages are skewed by outliers. We squint at p-values. We count stuff. We use stock Excel functions to draw lines through scatter plots. We interpret charts, lecture product managers about statistical significance, warn people that correlation doesn’t equal causation, and remind everyone that proxy metrics are the map and not the territory.
This is all a pretty weak justification for putting math on as high of a professional pedestal as we do. Much of our mathematical work is the stuff of grade-school arithmetic, and is a bar that most college graduates easily clear. While there are exceptions, the equations we write are just algebra; our favorite algorithm is division. Yes, math is useful, but our minds don’t need to be that beautiful.
In other words, it’s not our ability to do fancy math that makes us effective, but our ability to apply basic math. The industry’s slow pivot away from technical skills and tools and towards collaboration and internal politics3 is a reflection of the same dynamic: Math doesn’t separate the good analysts from those who struggle. We often operate like intelligence analysts, looking for connections in a sea of messy evidence, rather than statisticians trying to parse endless regression readouts.
This is hardly a controversial point. If most of us where asked by a junior analyst if they should invest in understanding the business, or in understanding various probability distributions and the fundamental theorem of calculus—which is high school stats and math, by the way—we wouldn’t flinch in recommending the former.
Moreover, excellent written and verbal communication skills are a nearly universal requirement on analytical job postings. But we don’t require a communications degree, and don’t train people to write. These sorts of skills—presenting, persuading, and collaborating, to say nothing of having an understanding of the business domain in which most analysts work—are seen as things we can learn on the job. They’re skills that can be layered on top of a “math person.” It is only for math and its sister requirement, “technical skills,” that we want more formal qualifications—despite, I’d argue, it being easier to teach a great communicator introductory statistics than it is to teach a great mathematician how to be organizationally effective.4
In that context, the curious thing about the HBR article isn’t its lowly positioning of mathematics and statistics; it’s our triggered reaction to their rankings. It’s almost as if our fixation on math was never about the subject’s substance, but its signaling.
Shape rotators sell words
Every culture has its codes. One of Silicon Vally’s is the language of false and unnecessary quantification. We don’t change our minds; we adjust our Baysian priors. We don’t know something; we assign it a high epistemic probability. One thing isn’t way bigger than another; it’s an order of magnitude bigger.5 We don’t think; we create mental models. We don’t tell stories; we share Ns of 1. There aren’t lots of small things and a few big things; there’s a power law.6
Like the business jargon it’s usually wrapped around, these phrases only appear precise. But they describe comparisons of estimates of predictions that use assumptions—I mean, priors—that are flatly unquantifiable. By describing them in this language, however, and presenting them in color-coded spreadsheets or on two-by-two grids, we can pretend that they represent some sort of objective science, and aren’t just rhetoric by another name.
In doing so, we math people can stifle debate against the qualitative luddites. I have numbers, you don’t, and tech folk hero W. Edwards Deming said that means I win. Never mind if the figures behind my slang are entirely made up; that just makes them all the more difficult to refute.
In cultures that revere math and science—not as disciplines, but as vibes—this vocabulary can be a powerful weapon. While artists are unlikely to be swayed by artificial cost-benefit calculations,7 among business leaders and data-driven companies, this language has standing.
Our deference to math, and particularly its more advanced strains, isn’t about its practical business value. It’s about protecting this culture. It’s about settings the terms of our internal debates, and ensuring that those who appear to “bring data” maintain their power in the professional order.8 Math is a useful skill, and an even more useful sorting hat—and the more we venerate the former, the better it becomes at the latter.
Bullets of reason
So what, though? Is this bias so bad? Is it not better to roughly quantify the unquantifiable than to discount math’s value?
Again, the HBR article is instructive. Rather than making a substantive, and potentially quite reasonable, claim as to why organizations should invest in data visualization expertise over mathematics training, they simply put the two on a plot. They shortcut a real argument with a smokescreen of manufactured data and feigned rigor. And like a founder trying to sneak a scatterplot of logos by an critical investor, they pushed their luck too far and someone called their bluff.
If we valued persuasion and storytelling as much as math, this wouldn’t happen. If we demanded that data needs to be explained in simple words as much as words need to be supported by data, we wouldn’t assume that a few lazy graphs—the bullets of analytical argumentation—are sufficient. If HBR’s editors weren’t blinded by a mathematical bias, they wouldn’t have printed themselves on the losing end of an immortal poster.
Beyond that, math can make us jerks. Shortly after college, when I was no longer just a math person but an official credentialed math major, I remember having several discussions with various family members about voting. I smugly trotted out a few basic statistics about how your vote is very unlikely to ever affect an election. The math was sound, but missed the point: People don’t just vote to sway an election. But I refused to hear these points, or even engage with them, because they weren’t quantified. I argued with math; they didn’t; Q.E.D.
In today’s society, filled with its “mathematically-focused jobs,” it’s all too easy to do the same. It’s all too easy to dismiss qualitative reasoning—and, by extension, people who don’t identify as math people9—simply because they don’t speak the right dialect. But, before reflexively defending the inherent necessity of mathematical expertise, we should make sure we care about it for right reasons. To put that in terms we might better understand: Math’s value follows a power law, and even in data roles, there’s an order of magnitude more of us on the left of the distribution than in its tail.
Fun fact: I was in the crowd for the original James Johnson poster.
Math is to data jobs as algorithms are to software developers: It sounds like what we do, but in practice, we’re mostly trying to figure out why this one thing doesn’t match this other thing.
Katie doesn’t directly refer to this as politics, but I think it’s important to recognize that that’s what it is, and that’s not a bad thing. We often use politics as a pejorative, framing internal negotiations as a kind of unhealthy horse trading. But as messy as it sometimes is, politics is how stuff gets done. By avoiding it, we aren’t taking the high ground; we’re surrendering decisions to others.
You could argue that, while we don’t need advanced math, we celebrate it because foundational math is really important. Though I agree that it is, you could say the same thing about a slew of other professional skills. But would we react the same if HBR said that persuasive writing or basic financial acumen were things we could ignore? We might disagree with that piece, but I doubt we’d literally destroy it.
I particularly like when this is applied to unquantifiable concepts: Superhuman is better than every other email client by at least an order of magnitude. Politicians need to know an order of magnitude more about AI. There are two orders of magnitude more free speech on Twitter now that Elon Musk owns it.
And when we don’t use math, we’re not making stuff up; we’re reasoning from first principles.
This was awkwardly proven by another HBR article, in which Jerry Seinfeld was asked if McKinsey could’ve helped make Seinfeld. Sadly, there’s no video of Jerry’s reaction.
Is it a coincidence that this dynamic also reinforces tech’s existing gender and racial order as well? Surely it must be.
This can have particularly toxic effects, as people often see mathematical ability as a fixed part of their identity. “I’m not a math person” can easily become, “I don’t belong.”
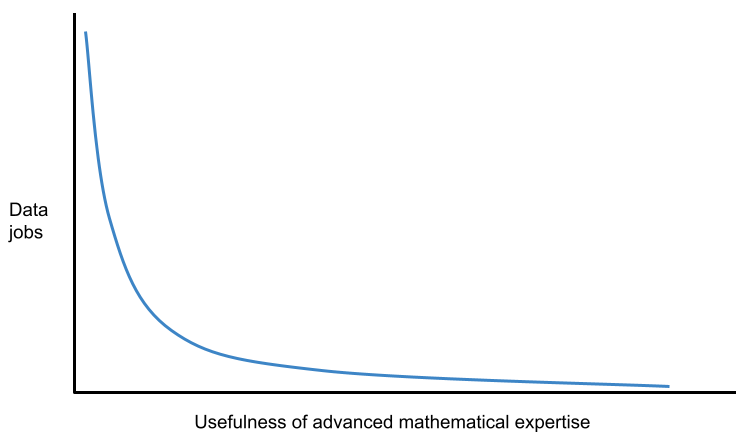
Benn, great post. My degree at UCLA was in economics and, as a tech CTO, I've used my skills in logic, reasoning and writing infinitely more than math. I have 2 sons pursuing a career in computer science and I take issue with their math-heavy curriculum. Our industry's over-rotation on math discourages a whole population from considering a career in CS and under prepares those who do for life in the real world.
Benn, excellent article; one which describes how I arrived in math from a desire to be a history professor. My parents were convinced that I would starve in my desired profession, and they had the means to enforce their beliefs. By my SAT and National Merit scores (there used to be separate tests), I was equally competent, and proved to be so. They were, sadly, correct! Far better to explain the outcomes of relatively simple math to those who were afraid of symbols, than to change an engineer's mind, even (maybe especially) when they were wrong. I can now enjoy my retirement in the knowledge that I can figure out a plausible answer to current problems/questions across a broad spectrum, and have the ability to see the flaws in the arguments of the many poltroons and idealogical statisticians among us. And I am still prepared to learn from real experts. Including about fishing and cooking.